运筹学 Part 1——线性规划问题求解方法

运筹学 Part 1——线性规划问题求解方法#

这个学期我选了大三的运筹学，所谓的运筹学，就是在约束条件下如何求解一个函数的极值。像CS229中的SVM部分(KKT条件推导)，而我们的最为简单的约束条件以及目标函数就是线性函数 ，因此线性规划问题的求解就非常的重要

线性规划问题的一般形式#

目标函数 ：由于目标函数为线性的，我们要求 $c^T x$ 的最值，由于 $max\ c^T x\Leftrightarrow min\ -c^Tx$ ,从而对于任意线性规划问题，**目标函数可以转换成 $min\ c^T x$

线性约束 ：对于我们的约束而言，可能有 $Ax\geq b, Ax=b, Ax\leq b$ ,对于等式是最好处理的，我们考虑将不等式化为等式=>考虑高中数竞中的小技巧:将差值设出来， $Ax\geq b\Leftrightarrow Ax-s=b, s\geq 0$ ,其中s的维度和A的行数相同。

同样的道理有 $Ax\leq b \Leftrightarrow Ax+t=b,t\geq 0$ 从而我们所有的约束条件都可以表示成 $Ax=b$ 的形式 (最多添加几个人工变量)

变量范围： 在线性约束中我们添加了若干个人工变量,这些变量的都是大于等于0的，因此我们希望对于原有变量也全部大于等于0.

• 对于某一个变量 $x_i$ 而言，如果 $x_i$ 有下界，那么用 $x'_i(x_i-low_{bound})$ 代替原有的 $x_i$ 即有 $x_i'\geq 0$
• 若 $x_i$ 没有下界，使用 $x_i=y_i-z_i,y_i\geq 0，z_i\geq 0$ 代替从而有所有变量都有下界0
• 如果 $x_i$ 有上界 $x_i\leq u_i$ ,添加人工变量 $y_i$ 以及约束 $x_i+y_i=u_i$ 此时有 $u_i\geq 0$ ,对于 $x_i$ 的处理方法同没有下界

经过以上的操作，我们有 \begin{align*} \min \quad & \mathbf{c}^\top \mathbf{x} \\ \text{s.t.} \quad & A\mathbf{x} = \mathbf{b} \\ & \mathbf{x} \geq \mathbf{0}. \end{align*} 这样的形式称为线性规划的一般形式

线性规划解的不同刻画(简略)#

我们来介绍几个概念

• 可行域 $P=\{x\in R^n|Ax=b,x\geq 0\}$ 称为问题的可行域
• 凸集 :一个集合P称为凸集， $\forall A,B\in P ,\lambda\in[0,1]\Rightarrow \lambda A+(1-\lambda B)\in P$

容易发现所有线性规划问题的可行域都是凸集

对于线性规划问题的解，我们在高中的时候做题，顶点，边界为常见的极值点的位置，我们想要刻画这个顶点概念

• 极点 ： $\exists C, \forall x\in P \Rightarrow c^Tx>c^T \hat{x}$ 此时我们称 $\hat{x}$ 为极点(一个多面体的一个角)
• 顶点 ：x称为P的顶点，如果 $\not\forall A,B\in P (A,B\neq x),\lambda\in [0,1], x\neq\lambda A+(1-\lambda) B$ (也就是不存在有点与它共线)

可以发现顶点和极点是”等价的”，但是在计算的时候并不方便，于是有

• 基解 ：如果x为n维向量，在P中的n个线性无关的约束构成的线性方程组有唯一解，这个解为P的一个基解
• 可行基解 ：如果基解在P中，那么称之为P的可行基解

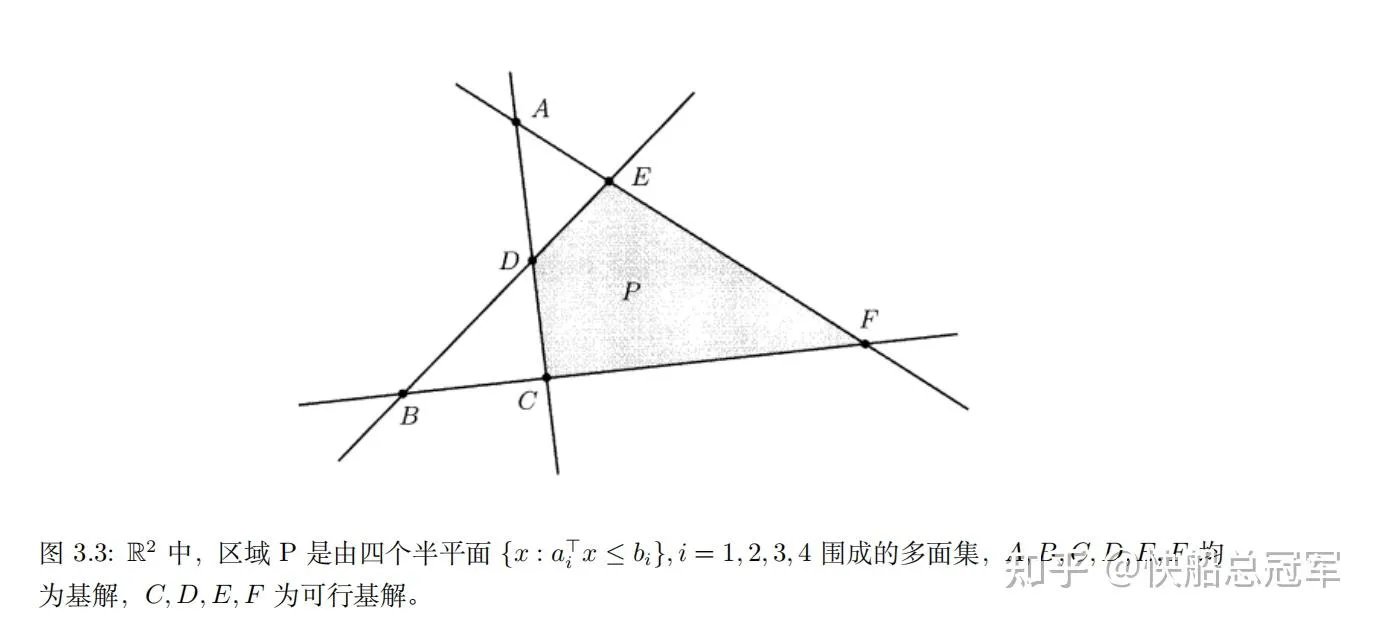
可以证明：在线性规划问题(凸集)中，极点，顶点，可行基解是等价的，对于线性规划的极值，要么在无穷处取到，要么可以在一个极点处取到

从而我们可以将一个不容易计算的** “顶点，角”**转换称计算一个线性方程组的问题。

对于这个定理的证明可以看我的手写笔记：

单纯形法#

如果我们直接将每一个可行基解求出来，然后计算其对应的目标值，总共的基解数目为 $C^n_m$ ，而对于求解一个线性方程组，也就是求逆的操作，复杂度为 $n^3$ ，总共就是 $C^n_m n^3$ ,太大了。

因此单纯形法的思路就是** 从一个基解开始，通过一个损失函数找到可以使目标函数进行改善的下一个可行基解，然后进行解的变换并继续迭代下去**

损失函数#

对于标准的线性规划问题，我们一个可行基解什么时候是最优的，此时我们借鉴** 理论力学中的虚功原理：找一个小的位移！！**

由于我们的可行基解可以看成若干个平面的交对应的顶点，如果想要移动到一个新的基解上，我们考虑的是进行** 顶点对应平面的替换**

即为如果 $x_B$ 是由 $A_1,A_2,...A_n$ 构成的，那么就对于平面进行替换成 $A'_1,A'_2,....A'_n$ 得到 $x'_B$

而对于平面的替换的话，参考排序算法，自然想到进行一一的替换 $(A_1,A_2,...A_n)\Rightarrow (A'_1,A_2,...A_n)\Rightarrow (A'_1,A'_2,...A'_n)$

从而可以做到依次的抛弃 $A_1,...A_n$ 这些平面

如果对于 $Ax=b,\tilde{x}=x+\theta d$ 进行可行基的划分,就是 $A=(B,N),x=(x_B,x_N)^T,c=(c_B,c_N)^T,d=(d_B,d_N)^T$

而依次替换一个平面就是在数学上的表示就是

$\begin{cases} d_j = 1, & j \in N, \\ d_i = 0, & i \in N, \; i \ne j , \end{cases}$

由于移动后的点需要满足整体约束(在这个多边形表面上)，有 $0=Ad=Bd_B+A_j\Rightarrow d_B =-B^{-1} A_j$

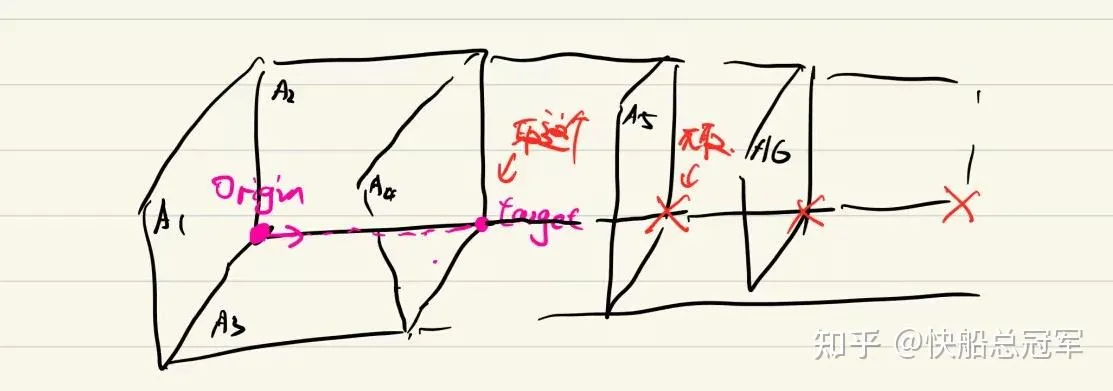
也就是图中的 $A_2,A_3$ 交线的方向向量

考虑进行一些小扰动，目标函数就有

$\begin{aligned} z &= c_B^{\top}(x_B + \theta d_B) + \theta c_N^{\top} d_N \\ &= c_B^{\top}(x_B - \theta \mathbf{B}^{-1} A_j) + \theta c_j \end{aligned}$

相比于原目标 $c^T x$ 变化量为 $z - c^{\top} x = \theta \bigl(c_j - c_B^{\top} \mathbf{B}^{-1} A_j \bigr)$

因此对于** 远离j这个基方向对于目标函数的影响，就是 $\hat{c}_j=c_j-c_B^{\top} B^{-1} A_j$** ，从而损失函数也可以理解成对于这个** 基方向的导数！**

转轴运算#

如果我们最优判定中，对于某一个可行基解 $x=(B^{-1}b\ 0)$ 可以计算其损失函数，如果对于某一个基方向 $x_j$ 有损失函数（导数） $c_j<0$ ，就说明对于j** 这个基方向进行移动，目标函数会减小**，这是我们需要的

具体操作为

对于 $\tilde{x}=x+\theta d,d=-B^{-1}A_j$ ，即为

$\begin{pmatrix} \tilde{x}_{B_1} \\ \tilde{x}_{B_2} \\ \vdots \\ \tilde{x}_{B_m} \end{pmatrix} = \begin{pmatrix} x_{B_1} \\ x_{B_2} \\ \vdots \\ x_{B_m} \end{pmatrix} + \theta \begin{pmatrix} d_{B_1} \\ d_{B_2} \\ \vdots \\ d_{B_m} \end{pmatrix}.$

• $d_{B_i}\geq 0$ 恒成立，如果有 $c_j<0$ ，那么在该点不是最值，沿着 $d_B$ 目标函数会不断增加，因此此时为无界解
• 如果存在i，有 $d_{B_i}<0$ ，那么在该方向上继续移动，会有移动距离的上限 ， $\theta \leq -x_{B_i}/d_{B_i}$ ,因此我们取最大的 $\theta$ ,记成 \begin{equation} \theta^* = \min_{\{i \mid d_{B_i} < 0\}} \left( -\frac{x_{B_i}}{d_{B_i}} \right). \end{equation}

从而我们得到了新的可行解

$\tilde{x} = \bigl(x_{B_1}, \cdots, x_{B_{r-1}}, 0, x_{B_{r+1}}, \cdots, x_{B_m}, 0, \cdots, x_j, \cdots, 0 \bigr)^{\top}$

从而通过替换基变量 $x_{B_r}$ 与非基变量 $x_j$ 得到新的可行解，这就是转轴运算

** 对于单纯形法的几何&代数的对应：**

• 可行基解 就是多面体的顶点
• 而损失函数(最优判定条件) 就是目标函数对于变量 $x_j$ 的导数
• 每一步我们都找到一个 $\dfrac{\partial c^T x}{\partial x_j}(c_j-c_B^{\top} B^{-1} A_j)$ 小于0的方向 (对应第一部分)
• 然后沿着这个方向进行移动，直到找到第一个可行基解(转轴运算 )

记住这个图片之后，再翻译成代数语言就可以了

单纯形表法#

由于我们的单纯形法每一步将可行基解中的一个变量从大于0变成0，并且将另外一个0变成大于0

其对应的基矩阵 $B\Rightarrow \tilde{B}$ 每一次进行迭代之后会添加一列，再减少一列 ，可以发现 $B^{-1},\tilde{B}^{-1}$ 之间会有许多关联

考虑相乘，可以发现 $\mathbf{B}^{-1} \tilde{\mathbf{B}} = [ \mathbf{e}_1, \mathbf{e}_2, \dots, \mathbf{e}_{r-1}, \mathbf{u}_r, \mathbf{e}_{r+1}, \dots, \mathbf{e}_m ]$ 中， $u_r=-d_B=B^{-1}A_j$

因此只需要对于 $B^{-1}A$ 进行线性变换，将 $u_r$ 对应的列变成 $e_r$ ，就可以得到 $\tilde{B}^{-1}A$

更进一步，我们可以同时对于入基变量,损失函数(导数)，函数值进行同样的线性变换,组成一张表，每一步的操作就是对于表的线性变换

$\left[ \begin{array}{c|c} -c_B^\top B^{-1} b & c^\top - c_B^\top B^{-1} A \\ \hline B^{-1} b & B^{-1} A \end{array} \right]$

• Step1 找到导数小于0的index：在第一行中找到一个值小于0的值对应的列prepare index
• Step2 找到在该方向上的第一个”平面”：在prepare index这一列上找到比值 \begin{equation} \theta^* = \min_{\{i \mid d_{B_i} < 0\}} \left( -\frac{x_{B_i}}{d_{B_i}} \right). \end{equation}
  并且进行入基，出基操作

一个例子为

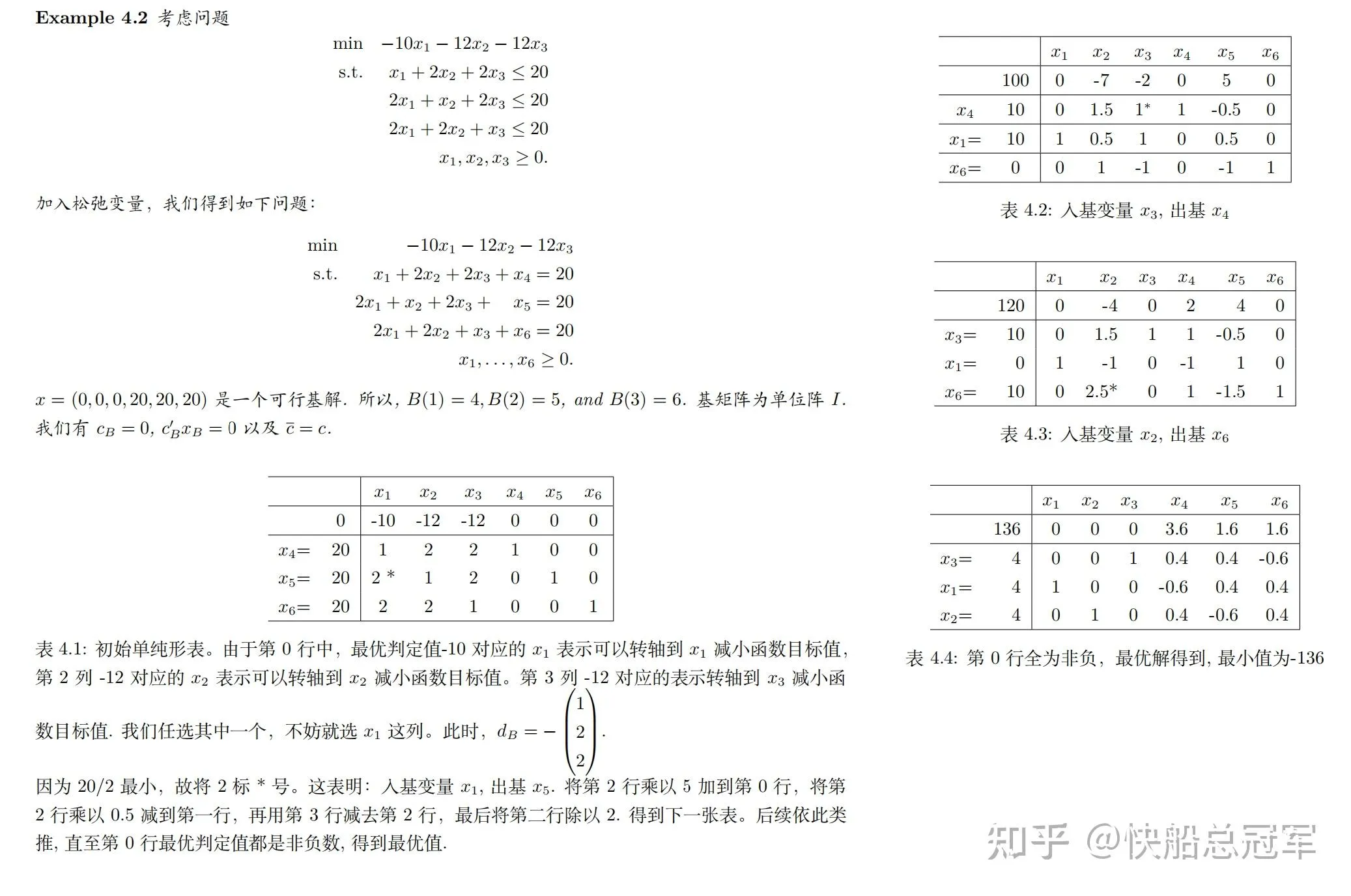
初始可行基解的寻找#

对于初始的可行基解的寻找，我们希望可以有类似与例子一样的基矩阵为单位阵的结构，观察到例子中的线性规划方程为 $Ax\leq b$ 的变种，即为 $Ax+y=b$ ,因此我们也进行同样的构造。考虑辅助问题

\begin{align*} \min \quad & \mathbf{1}^\top \mathbf{y} \\ \text{s.t.} \quad & A\mathbf{x} + \mathbf{y} = \mathbf{b} \\ & \mathbf{x} \geq \mathbf{0},\; \mathbf{y} \geq \mathbf{0}. \end{align*}

对于这个问题可行解非常容易发现为 $(x,y)=(0,b)$ ,从而可以构造单纯形表，最后得到最优解

如果我们的原问题有可行解存在，那么可以取 $(x,y)=(x,0)$ 此时有最小值为0，而由于 $y\geq 0$ 因此目标函数 $z\geq 0$ ，因此假设我们辅助问题的最优解为 $(\hat{x},\hat{y})$

• 若 $\hat{y}$ 大于0，那么有 $z=1^T y>0$ ,说明原问题没有可行解
• 若 $\hat{y}=0$ 此时得到的 $\hat{x}$ 就是一组可行解，从而可以进行正常的单纯形法

一些特殊的情况#

** 循环解情况：**

如果在单纯形表中入基变量中有多个0出现，那么就有可能发生两个变量 $i,j$ 来回入，出，入，出的情况，因此我们在进行入基变量选取的时候** Bland rule可以保证最后一定收敛**(可能会牺牲一点点的复杂度)

• 若非基向量中，存在多个 $\hat{c_i}<0$ 选取i最小的下标
• 出基的过程中，计算下标r使得 \begin{equation} \theta^* = \min_{\{i \mid d_{B_i} < 0\}} \left( -\frac{x_{B_i}}{d_{B_i}} \right). \end{equation}
  时，选取最小的下标 $B_r$

退化解情况：

如果我们的可行解 $x=(x_B,x_N),x_N=0$ 理论上 $x_B$ 有A.rank的大小，但是如果 $x_B$ 中有0的话，那么就无法分辨那个是入基变量，那个是别的了，对此我们可以：

** 直接从所有的 $x_i=0$ 中抽取若干个补充到 $x_B$ 中，这样找到的基矩阵也是满足要求的**

这样做有个前提是矩阵A是满秩的，这样对于任意抽取 $A.rank$ 列也是线性无关的，可以作为基矩阵。

代码实现#

关于实验要求以及我的代码可以参考我的github仓库

以上我们介绍了线性规划问题的求解思路，从问题的化简，到转换成计算机可以理解的语言，最后到单纯形法这种为了节省时间复杂度设计的东西，一节可能的特殊情况，同时我们也从几何角度理解了单纯形法的变换过程，最后我们进行了代码实现部分。总体而言，单纯形法还是非常漂亮美丽的算法