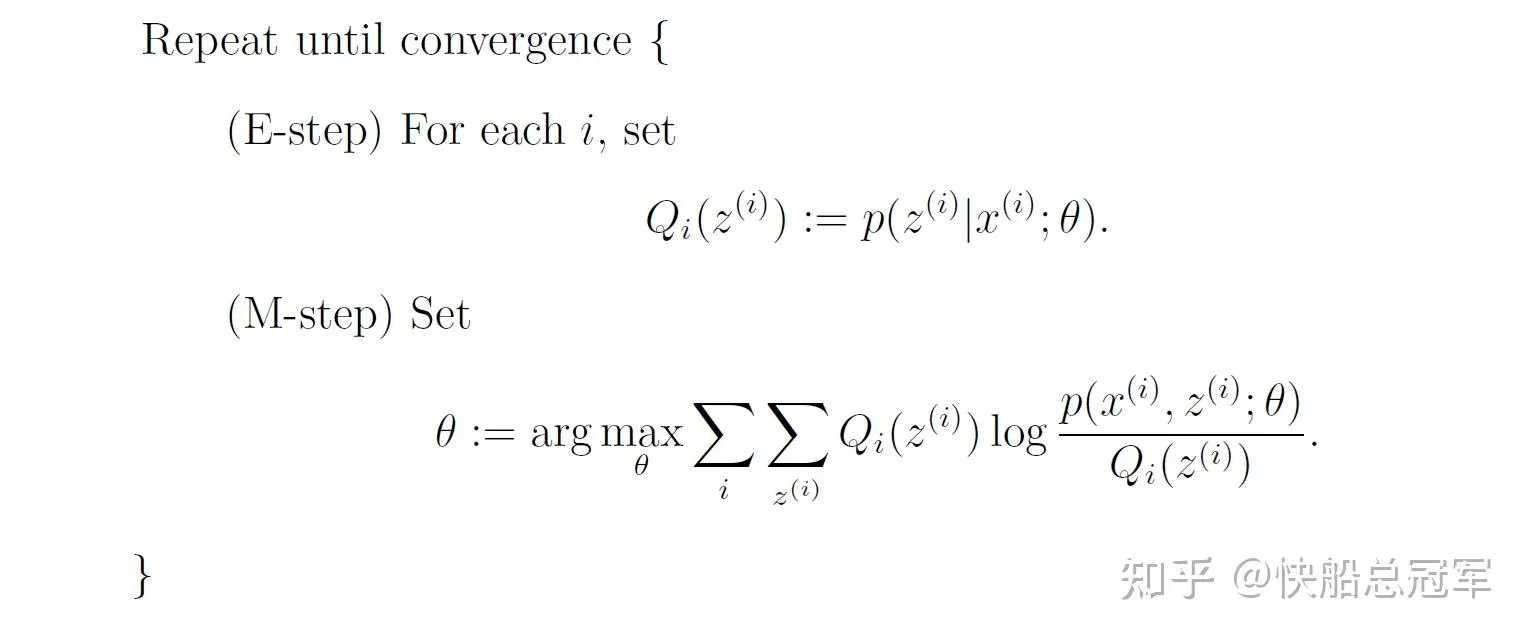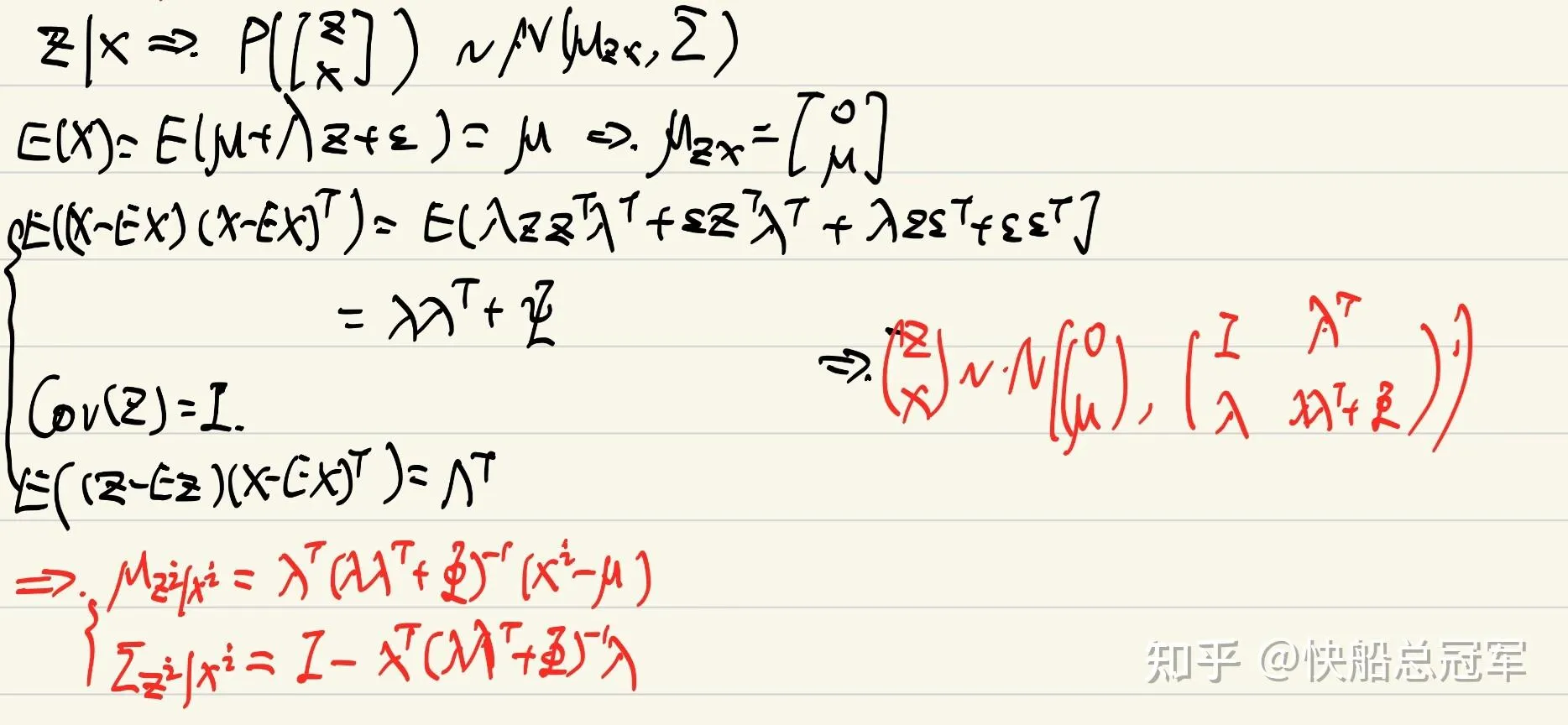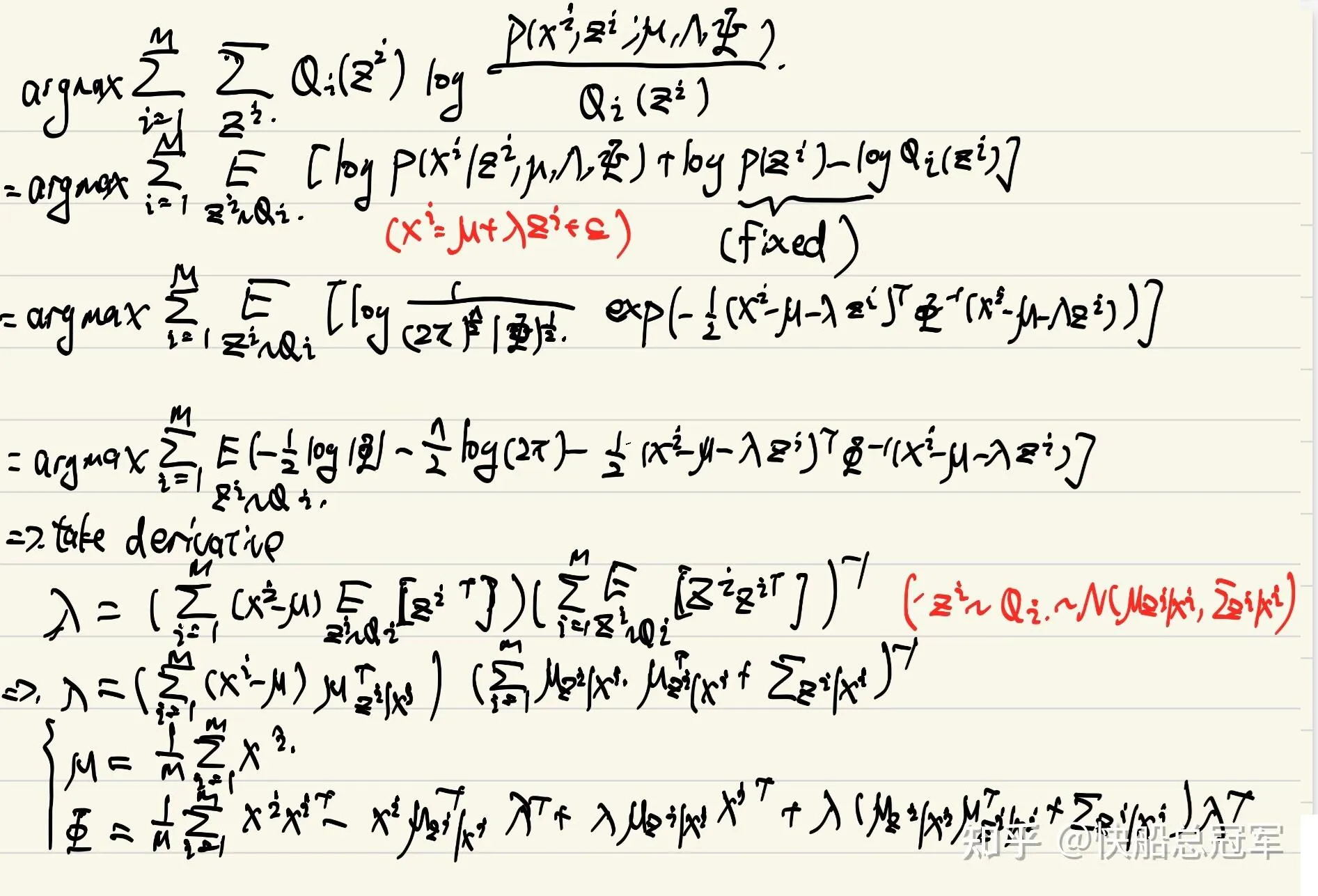CS229:无监督学习（二）——概率学习：高斯混合算法，EM算法以及Factor analysis • Bauklotze's World

上一篇文章中我们学习了无监督学习中不含概率假设的部分，但是使用MLE进行预测仍然是非常重要的预测方法，而之前对于无标签数据是通过假设距离 作为衡量因素，概率学习则是通过假设给定 $z,\phi$ 情况下的 $P(x|z^i,\phi)$ 去实现的，为了更加方便计算，我们会使用EM algorithm 去简化计算MLE的过程，但我们通过计算发现这只适用于训练数据量较大的情况，而对于数据维度比较大时，我们会使用Factor analysis 去代替分析进行特征提取。

Mixture of Gaussian#

仍然考虑对于给定 $(x^1,x^2,...x^n)$ ,将其分成k类的问题

对于之前Naive Bayes 的时候，我们是做出 $z^i$ ~ $Ber(\phi)$ 的假设，对于 $P(x^i|z,\phi)$ 可以通过训练数据去学习，而对于Mixture of Gaussian,我们需要对于 $P(x^i|z,\phi)$ 做出更多的假设才能得到相应的模型。

Assumption

$z^i$ ~ $Multinomial(\phi_1,\phi_2,...\phi_k)$ ,其中 $\Sigma^k_{i=1} \phi_i=1$
$x|z^i,\phi$ ~ $N(\mu_i,\Sigma_i)$ ,这个是合理的假设，对于一般的数据分布都是正态分布

从而代入

$\begin{aligned} l(\phi,x)&=log(\Pi^m_{i=1}P(x^i,\phi))\\ &=log(\Pi^m_{i=1}\Sigma^k_{j=1}P(x^i|z^j,\phi)P(z^j|\phi))\\ &=\Sigma^m_{i=1}log(\Sigma^k_{j=1}P(x^i|z^j,\phi)P(z^j|\phi))) \end{aligned}$

How to solve the parameters?#

如果我们已知 $P(z|x^i,\phi)$ 在supervised learning 中可以通过训练数据去得到，此时的参数为

$\begin{aligned} \phi_j &= \frac{1}{m} \sum_{i=1}^m 1\{z^{(i)} = j\}, \\ \mu_j &= \frac{\sum_{i=1}^m 1\{z^{(i)} = j\} x^{(i)}}{\sum_{i=1}^m 1\{z^{(i)} = j\}}, \\ \Sigma_j &= \frac{\sum_{i=1}^m 1\{z^{(i)} = j\} (x^{(i)} - \mu_j)(x^{(i)} - \mu_j)^T}{\sum_{i=1}^m 1\{z^{(i)} = j\}}. \end{aligned}$

而在此时，我们仍然是使用假设的方法：

求解Mixture of Gaussian

对于每一个循环中我们假设了 $P(z^i=j|x^i,\phi)=\dfrac{P(x^i|z^i=j,\phi)P(z^i=j,\phi)}{\Sigma^k_{i=1}P(x^i|z^i=j,\phi)P(z^i=j,\phi)}$ ,并保持它在该循环不变，更新相应的参数，最后该表达式会收敛到确定的参数值。

通过以上的步骤我们大致的得到了一个结果，但是至于为什么会收敛以及EM steps 的一般形式呢？

EM algorithm#

数学原理#

$Jenson\ Inequality:E(f(x))>f(E(x))$ 对于任何的凹函数成立，反之符号相反

琴生不等式 在高中数学竞赛中是一个常识性的结论，对于其数学证明可以参见《数学奥林匹克小丛书高中卷——均值不等式与柯西不等式》第一章的例题部分。

几何直观 上，以一个二次函数为例，就是对于凹函数，如果控制x1+x2的值不变，想要将 $f(x_1)+f(x_2)$ 的值更大，那么两者就要离得越远

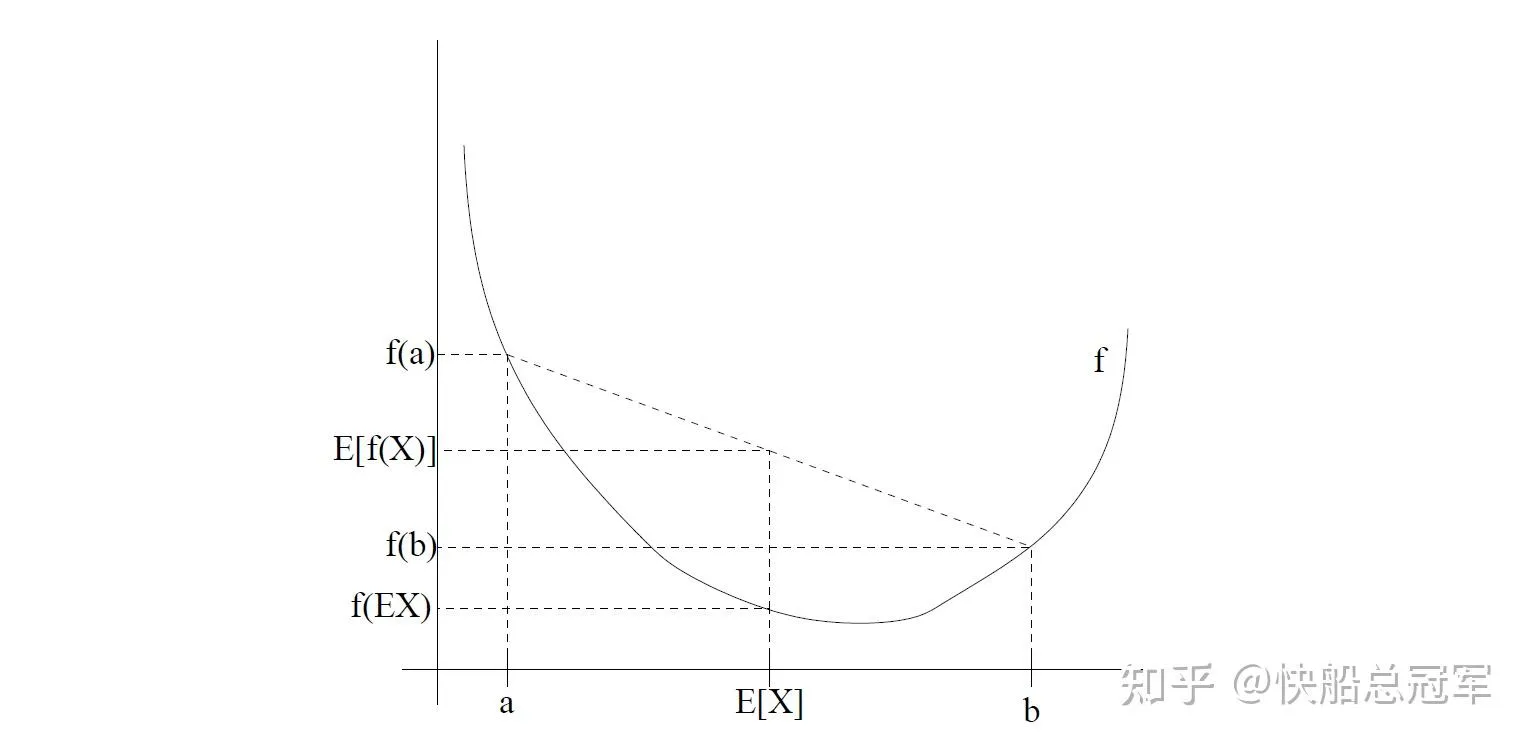
Jenson inequality

EM algorithm:#

假设对于给定 $x^i$ , $z^i$ 值的分布 $Q_i(z),\Sigma_zQ_i(z)=1$ ,则

$\begin{aligned} \sum_{i} \log p(x^{(i)}; \theta)& = \sum_{i} \log \sum_{z^{(i)}} p(x^{(i)}, z^{(i)}; \theta) \\ &= \sum_{i} \log \sum_{z^{(i)}} Q_i(z^{(i)}) \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})} \\ \end{aligned}$

由于log函数为凸函数，而我们想要求MLE的最大值，使用Jenson不等式，有

$\sum_{i} \log p(x^{(i)}; \theta) \geq \sum_{i} \sum_{z^{(i)}}Q_i(z^{(i)} )log( \frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})})$

使用右侧的函数作为损失函数更加方便计算。

对于 $Q_i(z)$ 怎么取呢？我们希望对于 $\frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}$ 方便计算，最好为常数，那么就有

$\frac{p(x^{(i)}, z^{(i)}; \theta)}{Q_i(z^{(i)})}$ ~c,结合 $\Sigma_zQ_i(z)=1$ 有

$\begin{align} Q_i(z^{(i)}) &= \frac{p(x^{(i)}, z^{(i)}; \theta)}{\sum_z p(x^{(i)}, z; \theta)} \\ &= \frac{p(x^{(i)}, z^{(i)}; \theta)}{p(x^{(i)}; \theta)} \\ &= p(z^{(i)} | x^{(i)}; \theta) \end{align}$

因此一般的EM algorithm的步骤 为

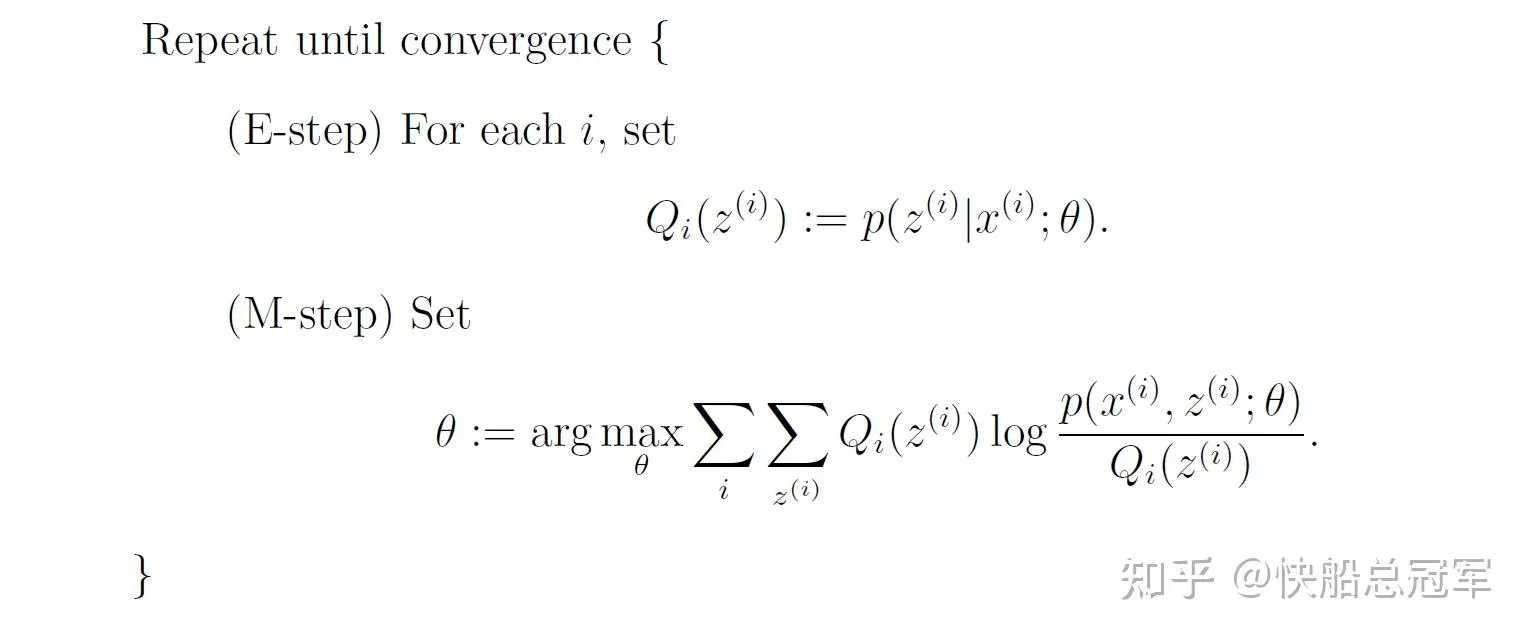
EM algorithm

Validate with Mixture of Gaussian#

在Mixture of Gaussian 中，我们就是通过Bayes 公式去计算 $p(z^i|x,\phi)$ 作为zi的分布，然后通过Jesnson不等式简化后的损失函数（同样是基于概率假设），使得对于每一个iteration之后，损失函数损失更小，参数更加接近真实值且反映出数据状况。（具体计算过程请见Problem Set 3 Solution ）

Factor analysis#

当数据维数大于数据的量时，由线性代数知识可知 $(x^1,x^2,...x^m)\in R^n$ 这些向量全部是线性相关的，则对于Mixture of Gaussian时有

$\Sigma_j = \sum_{i=1}^m w^i_j(x^{(i)} - \mu_j)(x^{(i)} - \mu_j)^T$ 行列式的值为0，此时在计算Gaussian的概率分布时 $\frac{1}{|\Sigma|^{0.5}}=\frac{1}{0}$ 这显然矛盾！这说明我们需要根据此时的数据特点做出些别的假设

预处理： 通过均值以及整体的方差将数据归一化

核心假设：

对于标签 $z\in R^d$ 表示认为标签为d类，同之前的总类数，有 $z$ ~ $N(0,I)$ (已经归一化了）
数据与标签成线性关系 $x=\mu+\lambda z+\epsilon$ ,噪声 $\epsilon$ ~ $N(0,\Phi)$

仍然是使用EM algorithm

E step： 计算 $P(z^i|x^i,\phi)$ ，由我们的假设，这是z和x的一个条件概率分布，也是正态分布，即有 $z^i|x^i,\mu,\lambda,\Phi$ ~ $N(\mu_{z^i|x^i},\Sigma_{z^i|x^i})$ ，我们通过协同概率去计算

对于条件概率我们有

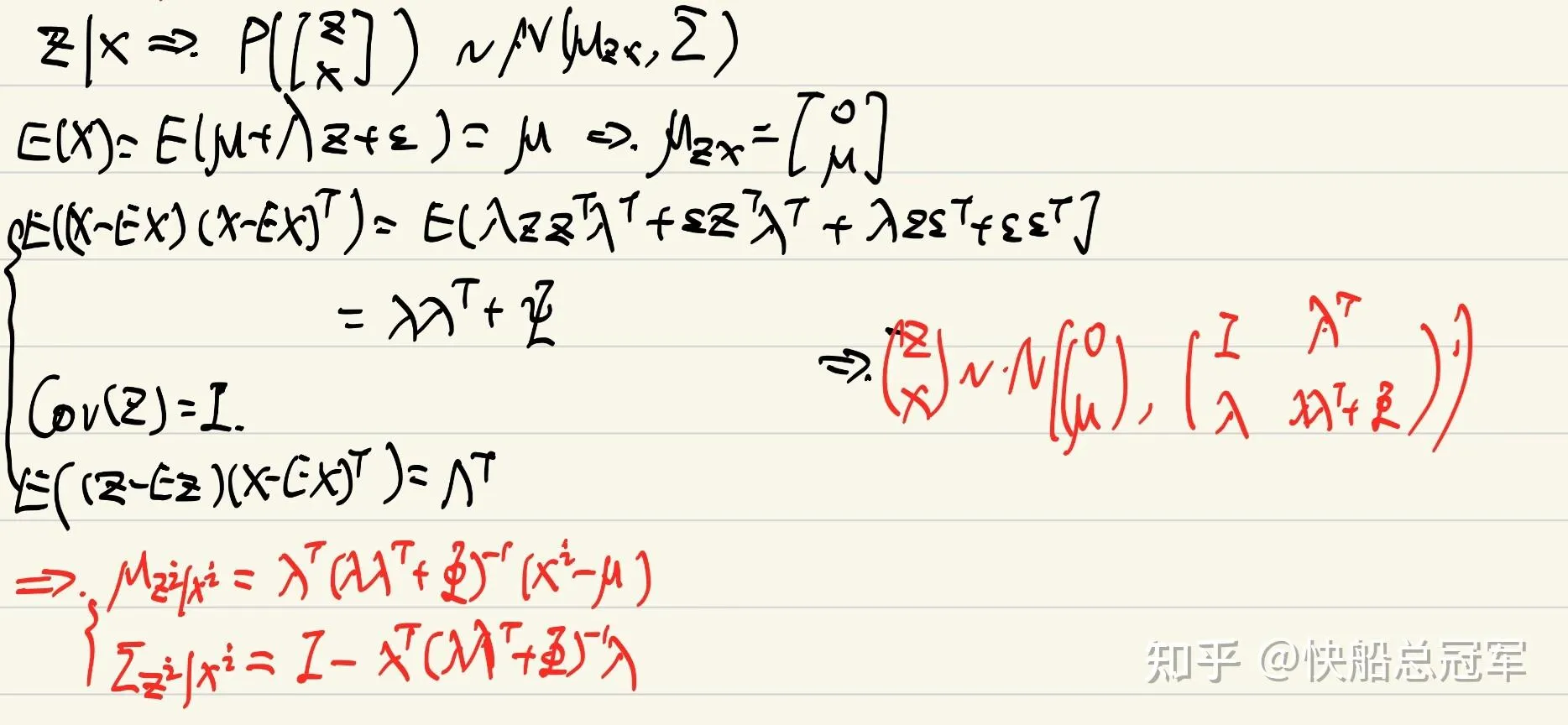
带入已知条件得到条件概率

M-step: 这里仍然是暴力计算，得到结果为

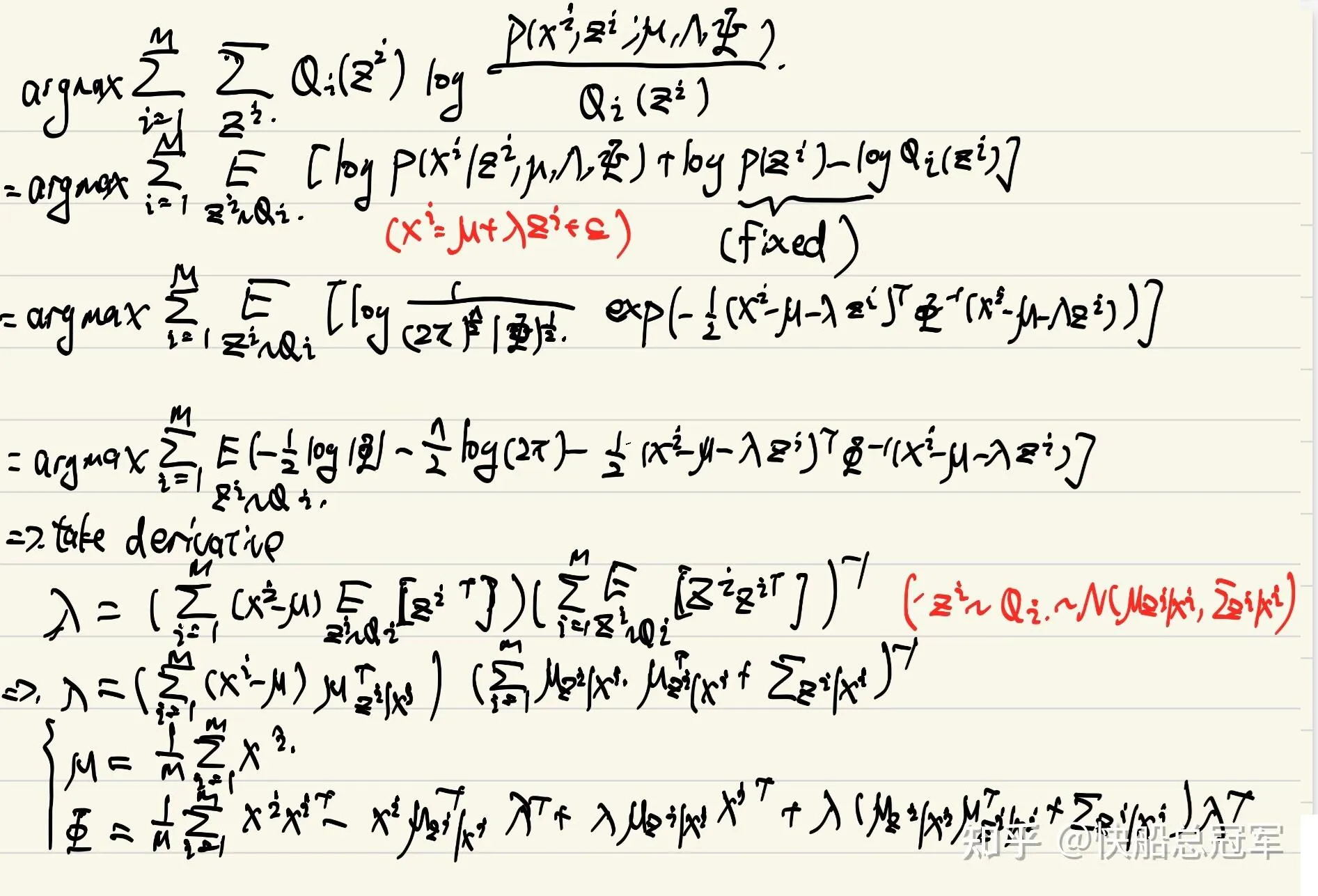
从而每个iteration迭代参数即可。对于Factor analysis可以将数据抽象成若干个特征，但是同时也可以反映不同特征的相关性，这点对于PCA是没有的。

在cs229中我们简要的学习了几种的无监督学习的算法，无论是无概率还是有概率，都是一定的假设，包括特征值，距离，高斯假设，以及对于特征的分布的假设并由此可以进行分类，特征提取任务。但个人感觉最重要的还是对于信息量 的问题。如果缺少了标签信息，就必须要一定的假设去补充，同样的，我们还可以添加一些别的假设，通过类似的方法，也可以得到新的无监督学习算法。